
|
unsubscribe |
|
|
|
What is a Fractal ? |
| A fractal is a rough or fragmented geometric shape that can be subdivided
in parts, each of which is (at least approximately) a reduced-size copy
of the whole.
The core ideas behind it are of feedback and iteration. The creation of most fractals involves applying some simple rule to a set of geometric shapes or numbers and then repeating the process on the result. This feedback loop can result in very unexpected results, given the simplicity of the rules followed for each iteration.
|
| Lets make a Fractal |
| Consider a triangle: |
 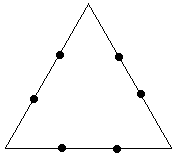 |
| Rule: add a smaller triangle to each edge : |
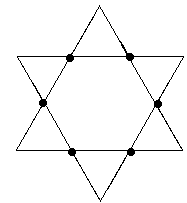  |
| This is the first iteration, now repeat the rule on each of the new edges: |
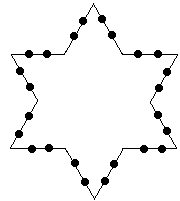 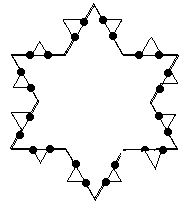 |
| If we continue this loops we get a beautiful fractal shape: |
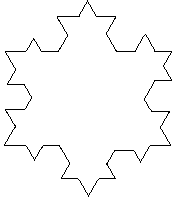 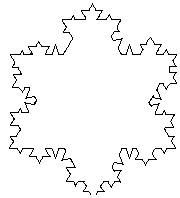 |
Finite Area, but Infinite Perimeter! |
| This process of iteration (looping) can continue for ever. Lets see
what is happening to the perimeter of the shape as we interate. If we define
the initial length of one side of the triangle as 1 unit then at the start
the shapes perimeter was 3 units. After the first iteration with the addition
of three small triangles the perimeter increased to 4 units. Then it went
up to 5.33 and our last image has a perimeter of 7.11 units.
We can make the observation that if we continue with this indefinitely we will end up with a figure that has a finite area, but an infinite perimeter. Think about that for a moment! This is a general property of fractals. Another property of fractals is self-similarity. If we look at the perimeter it looks similar - not the same - at all levels of magnification.
|
| More examples of Fractals: |
Dragon : |
 |
Snowflake : |
 |
Sierpinsky Carpet : |
 |
Its interesting to note that the total perimeter of all the holes (in
the original square) continues to increase as the remaining area (dark)
decreases. Eventually we will have something of no area but infinite perimeter
of all the holes?
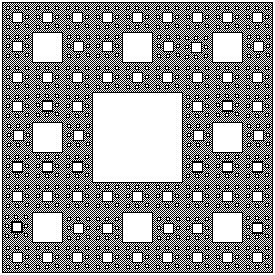 |
Sierpinsky Carpet : 3D Version |
 |
Sierpinsky Triangle : |
  |
  |
 |
Hilbert Curve : |
 |
| In the end, this one-dimensional line completely fills a two dimensional square and never once crosses itself in the process! |
Torn Square : |

|
Fractals in Nature |
Fractal geometry models natural objects more closely than does other
geometries.

|
Mandelbrot Set |
| The most famous fractal is the Mandelbrot Set.
The set is defined as those values of C which when iterated according to the complex number function Zn+1 <- Zn^2 + C with inital value Z= 0 + 0i result in a sequence that does not go off to infinity. Plotted, the set looks like:
|
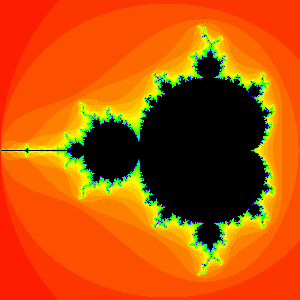 |
| The black region is the mandlebrot set, like other fractals its perimeter is infinitely convoluted, these regions can look beautiful when plotted. The colour regions represent numbers which when iterated "escaped" to infinity. How may iterations it took a number to escape is indicated by the different colours. Many of the images in our "Eternal Signs in Fractals" CDROM were generated from areas of the Mandelbrot and other similar Sets. |
Fractal Sound |
| Its been describes as "music composed by mother nature herself", but
what is it?
Fractal Sound is sound composed using the same types of feedback processes used to create fractal images.During fractal sound composition the numerical outputs from the feedback-process are mapped to sound parameters to produce melodies, harmonies, rhythms, textures, etc. Since there are numerous, if not an infinite number of, different ways to map the numerical outputs to these parameters the choice of a specific mapping has a substantial impact on the compositional results. Some people are amazed that this kind of mathematically generated music sounds much better than they expected. One reason is that self-similarity, a characteristic of fractals, translates well into music giving it that balance between predictability and randomness, between repetition and surprise, between the familiar and the strange. The sound track of our "Eternal Signs in Fractals" CDROM was generated solely from this process - you are listening to parts of the Madelbrot set! |